Comments (0)

By Gondozó, 2022. July 14 12:02

It turns out that the circulation on the wing is part of a much larger scheme of things. The circular part of the air flow is shed from the wings – mostly at the tips – to become the “trailing” vortices. If it were not for the viscosity of the air, the trailing vortices would continue clear back to the point on the ground where the flight began making what would look very much like a smoke ring. In reality, the trailing vortices are strong for at least 20 wing spans behind the plane and it is said that it would be a good idea to stay 10 to 15 miles behind an Airbus 380.

http://www.clker.com/inc/svgedit/svg-editor.html?paramurl=/inc/clean.html?id=41621

http://www.google.hu/imgres?start=119&hl=hu&safe=off&client=firefox-a&hs=HkY&sa=X&rls=org.mozilla:en-US:official&biw=1280&bih=846&tbs=itp:clipart&tbm=isch&tbnid=jTZvd8KyNIMVcM:&imgrefurl=http://www.clker.com/clipart-41621.html&docid=4hZYX-Qe9UuqHM&imgurl=http://www.clker.com/cliparts/e/e/2/9/1258128643633428473wirelizard_Top-down_Airplane_View.svg.hi.png&w=600&h=460&ei=jY6qUOeYKdCSswbAo4CQCA&zoom=1&iact=hc&vpx=495&vpy=419&dur=2156&hovh=197&hovw=256&tx=118&ty=76&sig=100566674577999627358&page=5&tbnh=149&tbnw=194&ndsp=34&ved=1t:429,r:43,s:100,i:133

Az indukált ellenállás csökkenése érdekében számos berendezést fejlesztettek ki, melyek segítségével akár 6% energiamegtakarítást lehet elérni.

Csillapító tervezése:

Ha tudjuk, mekkora fesztávolságú gépet szeretnénk, meg tudjuk állapítani a szárny karcsúságát. A téglalapszárnyra vetítve a kapott eredményt meg tudjuk határozni a szelvények húrhosszát és a szárny alaprajzi területét. Innen adódik a csillapítónk területét is, ami körülbelül 1/6 – 1/4 a szárnyfelületnek. Aszimmetrikus, felhajtó erőt termelő profil esetén akár 1/2 -e is lehet a szárnyfelületnek. Ugyanakkor a csillapító rosszabb körülmények között repül, mint a szárny, ezért nem érdemes túlzásba esni. Tehát a csillapító területét a következő képlet alapján számoljuk:

ahol az S a szárny területe (dm²), a pedig elrendezéstől függő tényező, mely 2,3 és 4 között szokott lenni rövid orrú, rövid törzsű gépeknél. Hosszú törzsűeknél elérheti akár a 15 értéket is. Összeadva a szárny és a csillapító vízszintes síkra vetett vetületét kapjuk meg a modell összes vízszintes hordfelületét.

Itt következnek azok a halálosan unalmas és egyben ijesztő képletek. De nem kell megijedni, le vannak egyszerűsítve, és elegendő hozzájuk az egyszerű számtan. Egy mezei számológép kell majd hozzájuk, egy ceruza, egy papírlap és egy radír, ha újra kell valamit számolni. Jó, ha van a számológépen gyökvonás, meg pár alap trigonometrikus függvény, mint

Aerodinamikai középhúr – az a húr, mely képviseli a szárnyat egészében, és amelyre úgy tekintünk, mintha fölötte hatnának a szárnyon ébredő erők. Természetesen, ez csak az eredők számításának egyszerűsítéséhez szükséges és a helyettesítési négyzet alakú szárny húrhosszát adja meg.

α – összesített állásszög (profil+indukált) (Cl – ounce)

C_D – összesített ellenállás együttható (profil + ellenállás) (Cl – ounce)

Keletkező felhajtó erő (Cl – ounce, V-mph, S -sqv.inch, sigma – levegő sűrűsége 1-0.7)

Szükséges felhajtó erő (Cl – ounce, V-mph, S -sqv.inch, sigma – levegő sűrűsége 1-0.7)

Modell sebessége (Cl – ounce, V-mph, S -sqv.inch, sigma – levegő sűrűsége 1-0.7)

Összesített ellenállás (Cd – ounce, V-mph, S -sqv.inch, sigma – levegő sűrűsége 1-0.7)

Összesített forgató nyomatés (Cm- ounce, V-mph, S -sqv.inch, sigma – levegő sűrűsége 1-0.7)

http://www.aerodesign.de/profile/profile_m.htm
http://adamone.rchomepage.com
http://tracfoil.com/tracfoil/de/autresD.html

Follow

Comments (0)

By Gondozó, 2021. December 19 22:45

nem emelő vízszintes esetén, az aerodinamikai középhúrron vett (eredő) nyomásközéppontban lenne az ideális súlyponthelyzet. de mivel a nyomásközéppont az állásszög függvényében mászkál ezért
célszerű a súlypontot a nyomásközéppont-vándorlás legelső lehetséges helyzete elé helyezni(persze praktikusan a kritikus állásszögig), mert így stabil repülési állapot áll be minden repülőképes állásszögnél.

emelő vízszintes esetén,  a súlypont a szárny nyomásközéppontja mögé kerül, mivel a vízszintes vezérsíkon is ébred felhajtóerő, amely részt vesz a gép nyomatéki egyensúlyának megteremtésében. vagyis a súlypont a két felület nyomatékának “zéruspontjában”  lenne ideális esetben, de praktikusan picit szintén előtte. ha a cél a stabil repülés.

Zsabrov -féle könyv alapján

Például 1. emelöprofilu vitorlázó esetébenn sik vizszintes csilapittóival valahol az elsö 1/3 hur között van (nem jo nagy emeloprofilu stabilzator és kis stabi nagy sebesseg eseten). 2. emelöprofilu csillapittoval a kilépö felöli 1/3 körül. Mint ahogy Jómukásember is irta valamiven a nyomásközpont elött kell legyen aminek a kiszámitása komoly mérnöki tudást igényel. Tehát mi egyszerü modellezök a tapasztalatokat kihasználva egyszerü algoritmusok alapján kisérletezünk és ismerve a modell viselkedését igyekszünk kikisérletezniaz optimális beállittást.

a közepes aerodinamikai húr meghatározásának módszere. Az igy kapott
AC (nyomásközéppont)-ot vetíti rá a repülőgép hossztengelyére.
Ezzel csak az a baj, hogy az AC pont és a GC (súlypont) egybeesése
esetén a gép neutrális viselkedést mutat, gyakorlatilag kormányozhatatlan
és repképelen.  Figyelembe kell venni a farokfelület módosító hatásait,
valamint a kívánt számszerűsíthető stabilitás mértéket is. Így az Ac és GC
soha nem esik egymásra, és a köztük lévő távolság a stabilitás
számokban kifejezett mértéke.

www.sry.atw.hu/40

http://www.sry.atw.hu/40hez.htm

http://users.atw.hu/sry/Spont.htm

http://users.atw.hu/sry/lateral.zip

Follow

Comments (0)

By anduur, 2012. September 20 12:11

Végre egy program, amely sokkal többet ér, mint amennyit elkérnek érte. A Profil 2 – egy szárny profil kezelő, rajzoló és elemző szoftver, melyet egyre több képességgel ruháznak fel a fejlesztői. Nagy bővíthető adatbázisának és szimulációs moduljának köszönhetően nagy segítséget nyújt a megfelelő profil kiválasztásában. A program segítségével megtervezhetjük a modell szárnyát és előkészíthetjük a rajzokat vagy a gépi vágási fájlokat, legyen szó balsa vagy habmagos szárnyról. Természetesen a többéves modellfejlesztői tapasztalatot soha sem lehet pótolni, de ha rendelkezünk megfelelő alaptudással és egy kis gyakorlati múlttal, elkezdhetjük szisztematikusan fejleszteni a gépünket, és akkor nélkülözhetetlenné válik a tervezőasztalunkon.
A fejlesztő csapat oldalán a szoftver 3 eltérő verziója érhető el: alap (base version) – lényegében hobbi szintű, kutatásra, fejlesztésre lett összeállítva, lehetőséget ad kiválasztott szárnyszelvények importálására/exportálására több fájlformátumban, polárgörbék számítására, habvágási sablonok készítésére, dobozos szárnyak tervezésére; XT – közepes felszereltségű programgyűjtemény. Lehetőséget ad DXF fájlok importálására, illetve saját profilok fejlesztésére több metódus alkalmazásával, szárnyszelvények többoldalas nyomtatására. Pro – verzió fejlett eszközöket hoz, melyet lelkes modellezők, klubok és gyártók számára ajánlják. Megengedi a profilgyűjtemény szerkesztését, ipari szabványoknak megfelelő fájlformátumok kezelését, 3 és 4 tengelyes maró-/vágó-gépek munkafájljainak előkészítését. Ezzel a verzióval CD-n vagy USB kulcson megkapjuk az adatbázisban fellehető profilok előre kiszámított polárjait, ezzel lerövidítve a tervezésre áldozott időt.
Licencelésben szintén megfigyelhető a csapat rugalmassága. Azon kívül, hogy rendelkezésre bocsátottak egy idő limit nélküli próbaverziót korlátozott funkciókkal, még három licenc típus közül választhatunk: egy diákok és hobbi modellezők számára, egy a klubok, alapítványok, oktatási intézmények számára (egy felhasználós), és egy klubok, alapítványok, oktatási intézmények és gazdasági intézmények számára (megosztott).
A szoftver telepítése nem igényel különösen kiépített számítógépet. ODBC32.DLL hiányában elég letölteni az MDAC.exe-t a társaság oldaláról.

Airfoils management/Processing – talán ezek lehetnek a legfontosabb 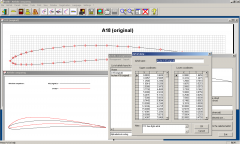moduljai a programnak, a profil kezelők. Itt megtekinthető több mint kettőezer profil, és ha pontosan nem tudjuk a nevét a profilnak, fejlett szűrőrendszer segítségével rákereshetünk töredékszavakra vagy akár profil tulajdonságokra hibamérték meghatározásával (-tól -ig). Bár teljesen elvárható volt és mégis meglepő, hogy az alap verzió mennyi profil szerkesztési lehetőséget nyújt. Természetesen, hogy csak azután, hogy kiválasztottuk és klónoztuk a kiszemelt szelvényrajzot, már  szerkeszthetjük is. Ez akar táblázatos formában, ívek adatainak módosításával, akár grafikus módszerek egyikével tehetjük meg (mert kettő is van: külső kontúr vagy vastagság és középvonal szerkesztése). Ezenkívül végezhetünk hibridizációt is, vagyis két egész profilból vagy részeiből készíthetünk egy új profilt. Ha befejeztük a szerkesztést, akár össze is hasonlíthatjuk az eredetivel vagy több más profillal. Más programokkal való összeférhetőség miatt több formátumot importálhatunk a rendszerünkbe, illetve exportálhatunk ki. Áldott tulajdonsága a szoftvernek, hogy raszter grafikai elemzője is van, vagyis régi tervrajzból is bővíthetjük a gyűjteményünket.

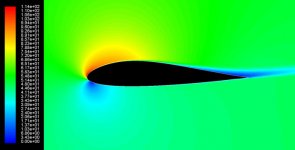
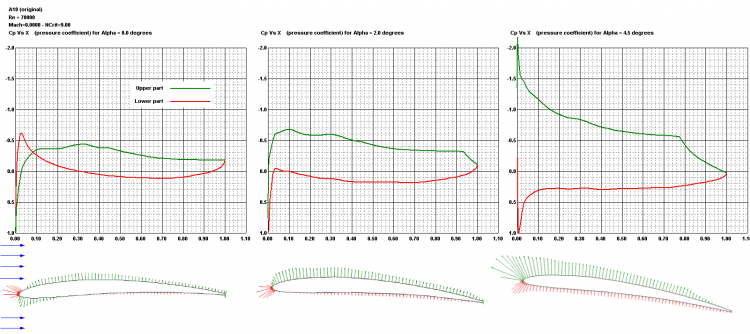
Polars – Xfoil (Mark Drela, GPL licenc) feldolgozó és elemző szoftverre épülő modul, mely professzionális analitikai módszerekre támaszkodva aerodinamikai számolásokat, elemzést végez el, legyen szó saját készítésű vagy szoftverrel érkező profilról. Ezen grafikonok az azokat olvasni tudók számára nélkülözhetetlen információt nyújtanak a repülőgép viselkedéséről, stabilitásáról, terhelhetőségéről. Az összehasonlító grafikonok a legjobb választást segítik elő bizonyos kritikus esetekre nézve. És ha már végeztünk a szárnyszelvények tanulmányozásával, ki is tudjuk nyomtatni a szelvényeket, ezenkívül a program segít megtervezni a bonyolultabb szárnyakat is, bordákkal, könnyítésekkel, borítással vastagságának figyelembevételével.

Miután kiválasztottuk a megfelelő profilt vagy profilokat, a megfelelő sebesség és felületi terhelés tartományban a Profili2 további segítséget nyújt a szárny szerkesztésében, immár közeledve a gyakorlati megvalósításhoz. Legyen szó az egyre kedveltebb hab és habmagos, vagy fából épített szárnyszerkezetekről, a szoftver segítségével létre tudjuk hozni a bordák és a szárnyfelek virtuális tervét és a kész terveket 1:1 arányban kinyomtathatjuk vagy fájlba menthetjük előre beállított papírméret alapján darabolva azt. Manapság egyre elterjedtebbé váló komputervezérelt alkatrészgyártásban (CNC) is segítséget kapunk a programtól. Végső lépésként a szoftver lehetőséget kínál három- és négytengelyes CNC fájlok kiexportálására, így megfelelő műszaki háttérrel, vagy egy erre szakosodott vállalkozást megbízva, a tervezett alkatrészekből könnyedén bordákat és más alkatrészeket kaphatunk, hosszadalmas műhelymunka nélkül.

Wing Panel Management. A szárnypanelek kezeléséhez szükséges funkciókat a főképernyő „Panels” menüpontja alatt a „Panel Management” alpontban érhetjük el. Amennyiben már rendelkezünk kész tervekkel, a programon belül itt találjuk-, nyithatjuk meg őket szerkesztésre, vagy hozhatunk létre új szárnyterveket. Szintén itt találhatóak az exportálási, nyomtatási és CNC beállítási funkciók is. Mivel ezen eszközök a gépi háttér viszonylatában jelentősen eltérhetnek, a funkciókat nem részletezzük, de teljesség igénye nélkül lehetőségünk van például a nyomtatási méretekkel kezdődően, vágásvastagság, marófejek alaki és méretbeli paramétereinek beállítására is.

Alapjában véve a Profili2 két típusú – trapezoid és elliptikus – szárnypanel tervezésére kínál lehetőséget, de a megfelelő paraméterezéssel e két kategórián belül szinte bármilyen formájú szárnyat megrajzolhatunk, az ívelt, hegyes teljesítményvitorlákétól, a „piskóta”, vagy delta formájú vadászokon át a szögletes műrepülő szárnyakig.

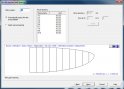
A szerkesztés menete a szárny alakjának és főbb alaki tulajdonságainak: fesztáv, húrhossz(ok), nyilazás, stb.) megválasztásával és pontos beállításával kezdődik és a további lehetőségeket lépéses rendszerben 9 további menüpontban érhetjük el. A szerkesztőablakok között végig oda-vissza lépegethetünk, javíthatunk. Jellemzően minden menüpont két fő részre osztható. Az ablak felső részén találhatjuk az adott szerkesztendő tulajdonságok paramétereit szám és szöveges mezőkkel, az alsó grafikus részen általában három nézet – felső, törzsoldali borda, szárnyvég oldali borda – közül választhatunk.

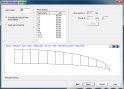
Második lépésben a bordák számát és távolságát állíthatjuk be. A szoftver képes automatikusan meghatározni az adott szárnyhosszhoz szükséges darabszámot és bordaközöket, de manuálisan is megadhatjuk a fenti értékeket.

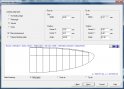
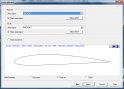A következő menüpontban nyílik lehetőségünk a gondosan kiválasztott szárnyszelvényt, illetve szelvényeket hozzárendelni a megtervezett panelünkhöz. A első és az utolsó profilt mi választhatjuk ki, az átmeneti bordákat a program automatikusan számolja ki és illeszti a szárnytervbe. Amennyiben bonyolultabb szárnyat tervezünk, a különböző szakaszokat külön-külön kell létrehoznunk.

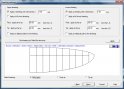
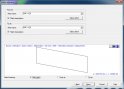
Negyedik lépés a torziós szerkezet megtervezése. Amennyiben 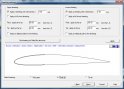ez nem szükséges az összes opciót üresen hagyva léphetünk tovább, de a Profili lehetőséget nyújt a szárny felső és alsó (jellemzően vékony balsa) borítását külön megtervezni, milliméterben vagy colban megadva annak fedését belépőéltől számítva, így teljes vagy részleges héjszerkezetű szárnyakat tervezhetünk. Természetesen a kialakításnak megfelelően a bordák tervrajzán is helyet kap a torziós balsa réteg.

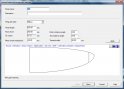
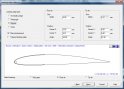
A szoftver logikai lépéseinek következő eleme a belépőél megválasztása. Fő opcióként a belépőél keresztmetszetét (forma, méret) határozhatjuk meg és illeszthetjük a bordák elülső oldalához x, y tengelyek mentén század-milliméteres pontossággal.
Hatodik lépésben a kilépőél szerkesztése következik. Háromféle verzió közül választhatunk, úgymint tömör és fedett élek, valamint kilépőél nélküli változat.

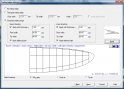
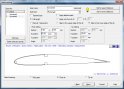
A tervezés vége felé közeledve jutunk el a merevítő(k) szerkesztéséhez szolgáló opcióig. Az egymást követő tervezőablakok közül ebben található a legrugalmasabb, legtöbb lehetőséget biztosító opciók együttese. 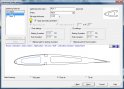Minden egyes merevítőt külön-külön tervezhetünk és helyezhetünk el a háromféle grafikus nézet segítségével, vagyis nemcsak a bordák x, y tengelyén, de bordától bordáig is. Hasonlóképpen állíthatjuk be a könnyítések alaki, méret- és számbeni tulajdonságait is, bár itt nincs lehetőség bordánkénti differenciálásra, amennyiben egy darabban terveztük a szárnyfelet.

A utolsó előtti opcióban az úgynevezett építő lábakat adhatjuk a bordákhoz. Ezek segítségével összeállításkor az összes alkatrész a megfelelő szögben és magasságban helyezkedik el a sablon felett.

Végezetül három fő nyomtatási opciót kapunk, amelyek ablakával zárul a szárnytervezés ezen szakasza. A szoftver generál egy felülnézeti képet bordákkal, merevítőkkel és torziós borítás rajzolatával, amit építési sablonként tudunk használni. Megkapjuk ezenkívül az összes borda rajzát 1:1 arányban, valamint a belépőélhez tartozó negatív mintákat. A beállított papírméret alapján a Profili automatikusan helyezi el, vágja és illeszti kinyomtatandó ábrákat oldalanként.

A tervezés végeztével visszatérünk a panellistánkhoz, ahol lehetőségünk van újraszerkeszteni azokat, vagy a fent említett módokon exportálni, illetve menteni különböző nyomtató és CNS készülékkel történő feldolgozás céljából.

Ahogy látható. ez a program kifejezetten a modellezőknek készült, de nem csak számukra lesz hasznos. Sok időt és munkát spórolhatunk meg a program használatával. Menet közben új megoldásokat is alkalmazhatunk kedvünk szerint, természetesen józan ész és biztonságos építmény keretein belül. Végül csak annyit szeretnénk üzenni a jó munkát helyett, hogy kellemes időtöltést kívánunk mindenkinek a tervező munkához :).

Follow

Comments (0)

By Gondozó, 2012. September 13 13:51

A kis sebességek aerodinamikája terén több mérnök és egyetemi professzor kitartóan dolgozik azon, hogy az analitikai módszerek minél jobban megközelítsék a tapasztalati eredményeket, megbízható támpontot nyújtsanak a tervezésben. A szerkezeti megoldásokkal együtt, szinte elkerülhetetlen jelleggel, magukkal hozzák azokat a tervezési megoldásokat, melyek jó modellrepülőgép megépítéséhez nélkülözhetetlenek. Esetünkben azonban a módszertan inkább közelítő jelleggel bír, mely segítségével meghatározzuk ugyan egyes paraméterek nagyságát de legalább 20%-os biztonsági tartalékkal kell számolnunk. A gép elkészültével, berepítés után derül ki csak, hogy megépített gépünk tudja-e nyújtani azt, amit megálmodtunk. Egy valamit azért mindig szem előtt kell tartanunk: csak jól megtervezett, megépített gépet lehet jól trimmelni!

Modelltervezés során a modell paraméterei, mint a szárnyfesztávolság, a húr hossza, a gép hossza, a legáltalánosabb és elsősorban megválaszolandó kérdések közé tartoznak. A modell teljesítménye a méreteivel együtt nő, a gép láthatósága javul, aerodinamikailag kedvezőbb körülmények között repül, de nehezebb a szállítása és sérülékenyebb is; 3 méternél nagyobb gépek esetén kompozit anyagok használata már elkerülhetetlen. Ezért a 1600-2400 mm szárnyfesztávolságú modell építése, tervezése és építése ajánlott azok számára, kik jól teljesítménnyel rendelkező és szállítható modellrepülőgépet szeretnének viszonylag rövid időn belül.

A szárnyra ható erők számításánál figyelembe kell venni azt, hogy a szárnyunk véges és a szárny végén “szivárognak” az erők, ráadásul, minél hosszabb a szárnyvég húrhossza, annál nagyobb a vesztesség. Ezen vesztességek mértékét a szárnyunk kialakításának jellemzői jelentősen befolyásolják. A végtelen szárnyra tett megállapítások ugyan igazak véges szárny esetében is, de a véges szárny fölött és alatta létrejött nyomáskülönbség megpróbál kiegyenlítődni, ezáltal az áramlatok oldalirányú mozgás is végeznek, térbeli áramlást hozva létre a szárny körül. Felülnézetben az áramlatok a véges szárny fölött a nagyobb íveltségű szárnyszakasz felé hajlanak, ahol alacsonyabb a nyomás (általában a törzs felé), míg szárny alatt az áramlatok a magasabb nyomású területekről a szárnyvégek felé hajlanak. A kilépőélnél a két réteg nyomása már közel azonos, de a részecskék áramlási iránya és sebessége eltér. A különböző irányú áramlások egyesülésekor a kilépő él mögött örvények keletkeznek, örvényfelület alakul ki. Különösen erős örvények alakulnak ki a szárnyvégek körül. Az indukált örvények energiát vonnak el a rendszerből és ezáltal csökkentik a szárny hatékonyságát, ezért kialakulásukat indukált ellenállás kíséri. Az áramlások oldalirányú eltolódása, és így az indukált ellenállás szorosan is a felhajtóerő keletkezéséhez kötött jelenségek, és alakulásuk annak nagyságától függ. Az indukált örvények hatására az egész áramlás iránya megváltozik, lefelé terül el. Mivel a nyomás hangsebességgel terjed, így a kitérés már a szárny előtt elkezdődik. Ennek köszönhetően a szárny valós állásszöge kisebb a geometriainál – ez az indukált állásszög. Newton törvényeit alkalmazva belátható, a felhajtó erőnk annál nagyobb, minél nagyobb légtömeget tudunk mozgásba hozni!

Ha már eldöntöttük, milyen fesztávolsággal fog bírni a modellünk, akkor következhet a szárny oldalviszonyának a meghatározása (jelölése görög labda [Λ] vagy AR). Az oldalviszony egy dimenzió nélküli szám, és a szárny karcsúságát jellemzi. Téglalap alakú szárny esetén ez a szárnyfesztáv és a húr hosszának a viszonya (), egyéb formájú szárny esetén a következő a fesztáv négyzetét osszuk a szárny területével:

ahol az S – a szárny alaprajzi területe, a b – a szárnyfesztávolság, l – profilhúr hossza. (A méreteket általában dm-ben számoljuk)

Indukált ellenállás tényezőjét a következő képlet szerint állapítjuk meg:

ahol c_y – a profil felhajtó-erő tényezője, δ – szárny alaki tényezője: ellipszis – 0; trapéz – 0,05-0,1… . Képlet alapján kijelenthető, hogy az indukált ellenállás nagysága a felhajtóerő-tényező négyzetes arányban függ, márpedig a szabadon repülő és vitorlázó gépek Cy értéke nagy, ezért indukált ellenállásuk csökkentése modell teljesítménye szempontjából jelentős lehet.

Számos kísérletben kimutatták, hogy az oldalviszony fontos szerepet játszik a felhajtóerő és az ellenállás alakulásában. Ahogyan az a grafikonból is kitűnik, kisebb oldalviszonyú szárny esetében ugyanolyan felhajtóerő eléréséhez nagyobb állásszög szükséges. Az indukált állásszög akár 3-5° is nagyobb lehet végtelen szárny esetében vett effektív szöghöz képest. A grafikonokból az is kiderül, hogy bár a karcsú szárny hatékonyabb a felhajtóerő termelésében, de emellett kisebb állásszögnél esik át. Ellenállás tekintetében a karcsú szárny előnyösebb.

Ezután teljesen természetesnek hat az a kérdés, hogy mégis mennyi legyen modellünk AR értéke, de a válasz nem olyan egyszerű. Ugyanis, minél nagyobb az oldalviszony, annál karcsúbb a szárny, annál kisebb az indukált ellenállás (kisebb nyomáskülönbséget kell kiegyenlíteni). Egyúttal, ha ugyanazon szárnyfelület esetén növeljük a szárny karcsúságát, csökken az áramlás lefolyását jellemző Reynolds- szám (rövidül a húrhossz). A következő nomogram gyakorlati kísérletekre támaszkodva, segítséget nyújthat a helyes érték választásában.

A gyakorlatban jól bevált értékek a nomogram zöld területen találhatók. Berajzolt minta szerint egy 2650 mm fesztávolságú modell esetén az oldalviszonyt 10,5 és 16,5 értékek között vehetjük fel, az ajánlott értékek azonban 12,5 és 15 közé esnek. Tehát az oldalviszony mindig a modell méretétől függ, és úgy kell megválasztani, hogy a legkisebb szelvényhosszúságú rész is a kritikus Re szám felett repüljön. Ahogy a modell-aerodinamikai kutatások nyomán kis Re-számoknál egyre stabilabb és kellő felhajtó erőt szolgáltató profilok jelennek meg, úgy a megengedett és ajánlott terület maximális határai egyre feljebb kerülnek a jelenlegi képhez képest. Figyelembe kell azonban venni azt is, hogy a modellünknek mekkora a káros ellenállása – a modell nem emelő részeinek az összesített ellenállása. Nincs ugyanis értelme az indukált ellenállás végtelenbe menő csökkentésének, ha nagy a modell káros ellenállása. A teljesítmény vitorlázók káros ellenállása igen kicsi a többi modellhez képest (nincs légcsavar, nincs hengerfej, stb.), így az indukált ellenállás a modell összellenállásának a felénél is nagyobb lehet, ezért ilyen modelleknél indokolt az indukált ellenállás-csökkentés.

Erő hatására a szilárd testek méretüket, alakjukat megváltoztatják. Nincs ez másként a szárny esetében sem. A szárny igénybevétele a szárnytőnél a legnagyobb. Ezért nem minden merevítőt szükségeltetik végig vinni a szárny teljes hosszán, a borítást is vékonyabbra lehet készíteni a szárny vége felé, ezáltal könnyebbé téve a szárnyat. Ezért aerodinamikai, de legfőképpen szerkezeti okok miatt gyakran alkalmaznak trapéz formájú szárnyakat vagy szárnyvégeket. Három okunk is lehet, miért válasszuk a trapézformát: rövidebb a szárnyvégprofil húrja, és ezáltal az indukált ellenállása, egyenletesebb a felhajtóerő eloszlása a téglalap formajuhoz képest, különösen nagyobb állásszögeknél, könnyebb. Nagyméretű gépeknél trapéz szárny különösen ajánlott. Ezen szárnyak egyik jellemzője a λ trapézviszony– a legkisebb és a legnagyobb szelvényhúrok viszonya.

ahol l_v – a szárnyvég profijának húrhossza, l_t – szárnytőprofil hossza.

A véges szárnyon végbenő állandó nyomáskiegyenlítés és oldalirányú áramlás miatt egy véges téglalap alaprajzú, elcsavarás mentes szárnyon a felhajtóerő nem oszlik el egyenletesen, hanem a szimmetriasíktól a szárnyvégek irányába haladva fokozatosan csökken. Ugyanakkor a leáramlás sebessége, az indukált ellenállás nő a szárnyvégek irányába. Ez azt eredményezi, hogy teljes azonosság ellenére a véges szárny közepes c_y kisebb a végtelen szárny értékéhez képest. Az erők eloszlásának ismerete repülőgép tervezés szempontjából nagyon fontos.

[kép]

Az 1930-as években eleinte empirikus módon, trapéz szárny lekerekítése útján, később pedig Prandtl áramlástani elméletére támaszkodva, matematikai alapokon is bebizonyították, hogy az elliptikus szárnyforma szolgáltatja az optimális aerodinamikai viszonyokat: a felhajtóerő a szárnyvégek felé haladva csökken nullára, a leáramlás pedig állandó szárnyvégtől szárnyvégig. c_ind=c_y²\πΛ képlet alapján az indukált ellenállási tényező ekkor a legkisebb.
Ilyen szárnyaknak az a hátránya, hogy bonyolult a megépítésük, hiszen bordapáronként újra kell tervezni a szelvényeket. Ezenkívül nem csak a felülete ívelt, hanem a be- és a kilépőél is, átesésük hirtelen következik be, és eközben a csűrő felületek hatékonysága is jelentősen romlik. Ezért a gyakorlatban inkább a tégla és a trapéz, illetve ezen formák kombinációjából származó szárnyak dominálnak. Azonban az elliptikus formától való eltérés a hatékonyság romlásához vezet. Belátható, hogy a szárny eltérő formái eltérő hatást gyakorolnak a folyamatok lefolyására, vagyis a tervezésnél számításba kell venni.

A véges terjedésű szárny ellenállása két részből áll: profil- és indukáltellenállásból, ezért az ellenállás tényezőjét a következő formula adja:

ahol c_y – a profil felhajtóerő-tényezője, c_x – a profil ellenállás-tényezője, δ – szárny alaki tényezője: ellipszis – 0; trapéz – 0,05-0,1… .

Az összesített szárny grafikonjából azonnal kitűnik, hogy létezik egy olyan v sebesség, amik az alaki és az indukált ellenmállás egyforma, és akkor az összesített szárny ellenállása minimális. Az eddig elmondottak alapján indukált ellenállás annál kisebb, minél nagyobb a szárny oldalviszonya és kisebb a felhajtóerő tényező.

Follow

Comments (0)

By Gondozó, 2012. September 12 10:37

A szárnynak tehát az a rendeltetése, hogy a repülőgép levegőben tartásához szükséges felhajtóerőt termeljen (Végtelen szárny aerodinamikája). Ennek az erőnek a létrejötte és nagysága a szárny geometriai kialakításától függ. A szárnyszelvények lehetnek szimmetrikusak, aszimmetrikusak, íveltek, S-formájúak és mind más-más tulajdonságokkal bírnak. Bár sok modellkészítő nem tartja feltétlenül szükségesnek egy új profil keresését a modellje számára, különösen, ha túl van motorizálva a masina, mert az nagyszerűen repül a régi szárnyprofillal és annak nagy ellenállása még hasznos is lehet leszállás közben. Azonban a vitorlázó gépeknél – ahol az egyetlen hajtóerő a gravitáció –, fontos szerepet kap a hatékonyság. Különösen igaz a megállapítás, ha még versenyeznek is a modellel.

Poláris diagram. Ahogy azt láttuk, hallottuk, éreztük már, eltérő állásszögeknél a levegőben haladó testen ébredő eredő erő is más. A profilok tulajdonságainak ilyen jellegű vizsgálatát először Otto Lilienthal kutató naplójában figyelhettük meg egy diagram formájában, mely egy ívelt szárny felhajtóerő nagyságának alakulását ábrázolta a légellenállás függvényében eltérő állásszögek mellett. Az állásszög sajnos nem mindenhol jelenti ugyanazt. Leggyakrabban a légáramlás irányvonala és a profil húrja által bezárt szöget értik, néha azonban a húr helyett az alsó alátámasztó vonalat veszik figyelembe. Ezért mindig tisztázni kell, mielőtt belefogunk a számolásokba, még ha az eltérés nem is olyan nagy.

Légcsatornás mérések eredményeként általában három grafikont kapunk melyek a felhajtóerő C_y, (néha C_f, C_l-ként jelölik ), ellenállás C_x (C_e, C_d) és nyomaték C_m alakulását ábrázolják különböző állásszögek függvényében. Mivel az ellenállás és a felhajtóerő változása nagyságrendekkel eltér, ezért a felhajtóerőt egy nagyságrenddel nagyobb skálán ábrázolják. A nyomaték ábrázolásánál a skála úgy van felvéve, hogy a pozitív értékek a belépő él felfelé, a negatív értékek pedig lefelé való tolásának mértékét mutatják.
Gyakran a felhajtó erő és az ellenállás viszonyát egy görbén ábrázolják. Ilyenkor a légerők eredőinek vektorait (F_r – jobb oldali képen szürke nyíl) rajzoljuk fel értelemszerűen úgy, hogy minden kezdőpontja az origóban legyen. Összekötve a különböző állásszegüknél kapott vektorok végpontjait, egy poláris görbét kapunk. Zsúfoltság elkerülése végett a C_x, és a C_y itt is eltérő léptekkel viszik fel a tengelyekre (általában 1:10-hez arány követendő). Így a diagram áttekinthető és jól kezelhető. Az előző cikkben bemutatottak alapján belátható, hogy vektorok vízszintes tengelyre dobott vetülete adja a C_x, függőleges tengelyre pedig a C_y tényezőket.

Ezen diagramokból sok hasznos információt nyerhetünk ki. Első ránézésre meg tudjuk állapítani, mi a felhajtóerő legnagyobb és legkisebb tényezője (C_y=f(α) minimuma és maximuma), milyen állásszögeknél kapjuk ezeket az értékeket (α_kr). Azonnal szembetűnik az is, hogy a példában vett aszimmetrikus szárny legkisebb ellenállását nem 0°-nál kapjuk, hanem szimmetrikus szárnyprofiloktól ellentétben, attól kisebb állásszögnél. Az is megfigyelhető, hogy az állásszög növelésével a szárny ellenállása eleinte csak kis mértékben, utána körülbelül 6°-8° környékén elkezd fokozatosan, α_kr kritikus szög közelében pedig meredeken nőni. Eközben a felhajtó erő meredek, majdnem lineáris növekedést mutat, és csak a kritikus szögnél lapul. Minél meredekebben emelkedik a görbe, annál nagyobb az 1° állásszögváltozásra jutó felhajtóerő változás. Kritikus szöget elérve az áramlások a szárny nagy felületéről leválnak. Ekkor a felhajtó erő hirtelen lecsökken, az ellenállás megnő, a szárny átesik. A legjobb siklószám és merülősebesség ugyanazon szárny esetében nincs ugyanannál az állásszögnél és egy pár extra vonal megszerkesztését igényli majd.

A legkisebb merülősebességet nagyobb állásszögnél érjük el, mint a legjobb siklószámot. Egy adott profil alkalmazása esetén elérhető legjobb siklószám értékét a kezdőponttól a polárgörbéhez húzott érintő adja meg. Az érintkezési ponthoz tartozó c_x és c_y értékeket elosztva kapjuk a legjobb siklószámot, a c_y/c_x itt a legnagyobb, a eredő légerő vektora ezen a ponton zár be a legnagyobb szöget az áramlás irányához képest. A legkisebb merülősebesség (és ezzel együtt a legkisebb siklószöget) úgy kapjuk, hogy egy érintőt keresünk a görbéhez, melynek a C_y metszési pontja pont 1/3-a az érintkezési pont c_y értékének. Ezen a ponton a c_y³/c_x² emelkedési szám éri el a maximumát.

Negatív tartományban ugyanez a helyzet, ugyanúgy megtalálhatók a “jelentős” pontok. Csak más értékeknél, mert a vizsgált profil aszimmetrikus. Szimmetrikus profilok esetében a pozitív és negatív tartományok grafikonjai tükörképei egymásnak. Megvizsgálva a leggyakrabban alkalmazott profiljainkat észrevesszük, hogy állásszög-tartományunk igen korlátozott, nagyjából 3° és 15°közé esik mindkét irányba. Az igazán jó teljesítmények sávja még ennél is sokkal szűkebb.

A szárnyszelvények légerőtani tulajdonságait elsősorban a geometriai kialakítása határozza meg, de ezen kívül számos olyan tényező játszik még közre, amelyeket közelebbről meg kell vizsgálni. Ilyen például a határréteg jellege, szárnyfelület simasága. Megvizsgálva a polárgörbék alakulását lényegében a repülőgép jóságát is megkörnyékezzük. Eltérő profilok grafikonjait összehasonlítva számos fontos megállapítást tehetünk profiljainkkal kapcsolatosan, azonban ezen erők összehasonlítását csak azonos megfúvási sebességnél célszerű elvégezni. Ezen ismeretek hasznosak lehetnek, ha kisebb mértékben igazítani szeretnénk a meglévő profilunkon.

A profil geometriai paramétereit általában százalékban adják meg a húr hosszúságának viszonylatában. Vagyis, ha a szárnyunk profilja 100 cm hosszú, akkor a 18%-os (vagy c=0,18) vastagság abszolút értékben 18 centiméteres vastagságot jelent. Különböző alakú szárnyszelvények légerőtani jellemzőit szélcsatorna kísérletekkel állapítják meg és profilcsaládokat alakítanak ki. A szelvények a nevüket általában az aerodinamikai intézet, néha a kutató személy után kapják: CAGI, NACA, Gö, Benedek. A szelvényeket családon belül számértékekkel jelölik, melyek a főbb geometriai jellemzőket adják meg. Így a NACA23012 nevéből a következő tulajdonságokat olvashatjuk le: íveltség 2%, íveltség maximuma 30%-on, vastagsága 12%, de a számozás családfüggő!

Felhajtó erő, ellenállás, nyomásközéppont és a Reynolds szám kapcsolata. (Re) – egy dimenzió nélküli szám, mely a kísérletben kialakított, és a gyakorlatban alkalmazott szelvény geometriai és áramlástani hasonlóságát adja meg. Profilok összehasonlításában nagyon fontos szerepet játszik, hiszen eltérő Re számoknál nem csak mennyiségi, de minőségi változásokat is figyelhetünk meg a szárny reakciójában. Mivel a szám sok paramétertől függ, és minden minden pontra figyelembe venni szinte lehetetlen, így közelítő számolást érdemes csak elvégezni nagyságrend meghatározása céljából, figyelembe véve, hogy a levegő átlag sűrűsége =14,4·10^-6 m²/s (15°C, 1013,2 mbar). Ezt követően a számot a test hossza (húr hossz) és áramlási sebesség (repülési sebesség) ismeretében könnyedén meghatározható. Belátható, hogy a modellrepülőgépek szempontjából a Re szám tartománya körülbelül 50 000 és 700 000 érték közé esik.

ahol – a közeg (levegő) sűrűsége (kg/m³); – az anyagra jellemző dinamikus viszkozitás (Pa·s), – a kinematikai viszkozitás (m²/s), – a húr hossza (m), – az áramlás sebessége (m/s).

Aerodinamikai kutatások korai szakaszában már kimutatták (1937, NACA rep.: 586), hogy a hasonlósági mutató értéke jelentősen befolyásolja a maximálisan elérhető felhajtóerő értékét, a szárny ellenállását és a profil átesés körüli viselkedését. A kísérletekben megfigyelték, hogy az állásszög növelésével a felhajtóerő azonos sebességgel növekszik ugyanazon profil esetében (függvény görbéje ugyanolyan meredek). Azonban nagyobb Re számnál a felhajtóerő maximuma és az átesés is nagyobb állásszögnél következik be. Általában elmondható, hogy ha a profil jól teljesít alacsony Re számnál, akkor a magasabb tartományban sem lesz vele gond.

A geometriai kialakítás és a tulajdonságok alakulása. Egy szárnyszelvény olyan jellemzői, mint vastagság (d), íveltség (f), azok maximumának relatív helyei (x_d, x_f) és a belépő él lekerekítésének sugara döntően befolyásolják a profil légerőtani tulajdonságait. Ezek közül talán a profil vastagságának a hatása a legegyértelműbb, hiszen ha vastagabb a profil, akkor a homlokprofilja, vagyis az áramlással merőleges vetülete nagyobb. A vastagság növekedésével azonban az ellenállással együtt a felhajtó erő maximuma is nő. A vastágsággal és annak maximális értékének helyét változtatva megváltozik a profil orrának lekerekítési sugara is, és ez elsősorban az α_k – kritikus állásszög környékén érezteti hatását. Ha ugyanis a lekerekítési sugár nagy, akkor az áramlatok nem válnak le hirtelen a szárny egész felületén, hanem a leválási pont fokozatosan halad a profil orra felé. A hegyesorrú, és általában vékonyabb profilokon, az áramlás zavartalan egy bizonyos szögig, utána lavinaszerűen leválik az egész felületen, hirtelen ellenállás növekedést és felhajtóerő csökkenést idézve elő. NACA 0006 profil esetén Re 70 000 számnál átesés körülbelül 5°-nál következik be. Átesés utáni felhajtó erő növekedés a szárny alatti nyomásnövekedéssel magyarázható.

A kísérletek tisztább képet nyújtottak arról is, miként viselkedik a szárny átesés előtt és legfőképpen utána. Lényegében átesés három főbb formáját különböztettek meg: hirtelen, éles és fokozatos átesés és természetesen ezek között számos átmenet létezik (lásd N60 profil tulajdonságait különböző Re számoknál). Eközben megfigyelték az átesés hiszterézis tulajdonságát is, mely azokra a profilokra jellemző, amelyeknél hirtelen felületi vonalvezetés változás (másként fogalmazva kis sugarú lekerekítés) található. A hiszterézis lényege, hogy az átesés után vissza is visszük a szárnyat az átesés előtti szögbe, az áramlások, és ezzel a felhajtóerő nem nyeri vissza eredeti értékét, míg a kritikus állásszög alá nem visszük a szárnyat. Egyes profilok különösen hajlamosak erre a “hisztire”, különösen, ha egy felületi maximumot egy hosszabb egyenes, vagy süllyedő (konkáv) szakasz követi.

Szimmetrikus profilokkal viszonylag alacsony maximális felhajtóerő érhető el, ezért csak a műrepülő repülőknél alkalmazzák illetve stabilizátorok kialakításánál. Az íveltség kialakításával, és annak értékének növelésével az elérhető felhajtóerő értéke is arányosan nő. Egy ilyen profil ellenállás-tényezője is kisebb, mint a hasonló vastagságú szimmetrikus profilé. Ezért a felhajtóerő növelése érdekében a középvonal íveltségének növelése gazdaságosabb megoldás. Hogyha különösen nagy felhatóerő-tényezőre van szükségünk kis sebességnél, akkor az íveltség maximumát célszerű a húrhossz utolsó harmadába helyezni. Az erősen ívelt profilok hátránya, hogy maximum elérése után erőteljesen átesnek és nagy a nyomásközéppont vándorlásuk.

Összegezve elmondható, hogy a profil vastagságának növelésével megnyújtja a felhajtóerő görbét C_y irányában, így nagyobb felhajtóerőt érhetünk el. Maximum pontjának előretolásával a görbe meredekebbé válik, és kisebb mértékben veszítünk a felhajtóerőből. Mindkét módosítás azonban alaki ellenállás növekedéssel jár előrehozott örvények miatt. Eközben a profil “nyugodtabbá” válik, ami az irányítást könnyebbé, kiszámíthatóbbá teszi. De hogy a vékony profilokat is dicsérjük, meg kell jegyezni, hogy alacsony Re számnál (30 000 környékén) és kis állásszögeknél a vékony profilú (~6%) vagy lapszárnyú gépek jobban teljesítenek, mint a gömbölyded társai. Analitikai módszerrel összehasonlítva sikerül kimutatni, hogy 200 000 értékig a vastag, 14-18% szelvények használhatóak sikeresen, de kezdve a 100 000 értéktől a többszázas tartományig a 8-12% vastagságú profil a preferált. Az íveltség fokozása pedig felfelé tolja a polárist, így a negatív tartományban kedvezőtlenebbül viselkednek. Ezért az ívelt profilok kevésbé alkalmasak a műrepülő gépek szárnyainak kialakítására. Mivel egyik érték sem növelhető korlátlanul tulajdonságok romlása nélkül, ezért az optimális választás körülbelül 10% vastagság és 2% íveltség környékén van, ahol c_y/c_x a legnagyobb értékeket vesz fel.

Minél nagyobb az íveltsége a profilnak, annál nagyobb a nyomásközéppont vándorlása, és annál nagyobb fogatónyomaték ébred a szárnyon, ami nagyobb stabilizátorokat igényel a kompenzáláshoz illetve változó megfúvásnál jelentős minőségi változást okoz. Nagyon ritka az egyszerű körszegmens formájú középvonal, általában bizonyos célnak megfelelően alakítják ki. Matematikai modellekre épülő profilok középvonala általában valamilyen szabályt követ. Például a NACA négyjegyű sorozata profiljainak középvonala két parabola szegmensből van képezve, melyek tangenciálisan vannak összekapcsolva a legmagasabb íveltség pontjában. Ezert a NACA profilokat nem csak íveltség magassága és helye alapján osztályozzák, hanem a középvonal sorozatokra is bontják. A legnépszerűbb a A=1 középvonal, mely egyenletes terheléseloszlást biztosít a profil mentén. A téma mélyebb megismeréséhez érdemes saját profilokat készíteni és elemezni tulajdonságaikat profilszerkesztő és elemző szoftverek segítségével (MacFoil, Airfoilplot, Compufoil, Xfoil, Profili).

A vastagság helyének módosításáról annyit kell tudni, hogy hatással van a lamináris áramlás megmaradására, ugyanis ez az áramlás marad, míg csökken a nyomás (vastagszik a profil). Nyomás növekedésével átvált turbulensé, melynek ellenállása nagyobb. Hagyományos szelvényeknél a lamináris áramlás a maximum a húrhossz 30%-áig tart ki. Ha azonban a maximális magasságot hátrább toljuk, a lamináris határréteg akár a húrhossz 40-60%-áig is kitart. Arra a kérdésre, hogy hol helyezkedjen el az íveltség maximuma,  a legnagyobb vastagság helye adja meg a választ. A gyakorlat azt mutatja, hogy ha a profil 30%-nál a legvastagabb, akkor az íveltség legkedvezőbb helye körülbelül a húrhossz 40%-ánál keresendő, a profil vastagsága a húrhossz 50%-ánál tetőzik, akkor az optimális íveltség helye 45% környékén keresendő.

Egy-két konklúzió az elméleti anyagból: 1. A jó átlagteljesítményt a minimális merülési sebességre való törekedéssel, vagyis minimális terheléssel és maximális c_y³/c_x² – emelkedési szám elérésével tudjuk biztosítani. Az emelkedési szám csak profil, állásszög és Reynolds szám függvénye. Ezért a vitorlázó modellek teljesítménynövelő lehetőségei a megfelelő profil, maximális c_y/c_xértékhez tartozó állásszög beállítása és hogy a modell a kritikus fölötti Reynolds-számmal repüljön. 2. Vitorlázók számára alacsony ellenállás és forgatónyomaték alacsony Rn szám mellet nélkülözhetetlenek. Műrepülő gépek számára szimmetrikus profil alacsony C_m értékkel a jó választás fokozatos átesési tulajdonsággal a szűk fordulók miatt. Emellett maximális C_y értéket kell keresni, ami csak elérhető.

Follow

Comments (1)

By Nykolett Kővári, 2012. August 30 12:29

A modelltervezés talán legkritikusabb, legfontosabb művelete a megfelelő szárnyprofil kiválasztása. Lényegében több ezer profil áll rendelkezésünkre, de legjobb csak egy van. Igen ám, de mi van azokkal a szárnyakkal, melyeknél több profilt is alkalmaznak? Igazából legjobb nem is nagyon létezik, mivel minden gép más és más. Ezért itt csak az irányelvekről, illetve az egyes kategóriákban jól bevált szelvényekről beszélhetünk, mert minden profilválasztás szükségszerűen magával hozza a kompromisszumot. A megfelelő profil kiválasztása első sorban azon múlik, mennyire értjük meg a leíró adatokat, és mennyire ismerjük a trendeket. Az aktuális felhajtó erő, a szárny ellenállása és a nyomásközéppont vektora az alábbi hat plusz egy paramétertől függ, melyek közvetett/közvetlen módon kapcsolatban állnak a szelvény profiljának kialakításával:

Sebesség – mindhárom érték egyenes arányban változik a sebesség változás négyzetével.
Szárnyfelület – mindhárom adat egyenesen arányban áll a felület nagyságával.
Húr hossz – Reynolds szám és nyomásközéppont egyenesen arányos a szelvény hosszával.
Állás szöge – a hasznos tartományban (0-felhajtó erőtől átesésig), mindhárom érték nő, de nem lineárisan (az alaki ellenállás bizonyos tartományban csökkenhet) az állásszög növelésével.
Oldalviszony – egyenes arányban van mindhárom paraméter értékével.
Szárny formája – többdimenziós hatása van mindhárom tulajdonságra.

Reynolds szám (Re) – egy dimenzió nélküli szám, mely a kísérletben kialakított, és a gyakorlatban alkalmazott szelvény geometriai és áramlástani hasonlóságát adja meg. A szélcsatornában mért profil adatai akkor igazak a szárnyprofilunkra, ha a vizsgált alanyok geometriailag hasonlóak (a felület kiképzésében is) és a Reynolds számuk is azonos. Ezt a számot a test hossza (húr hossz) és áramlási sebesség (repülési sebesség) ismeretében könnyedén kiszámolható. Mivel ez a szám sok paramétertől függ, így csak közelítő, nagyságrendi számítást érdemes elvégezni. Ezt a gyakorlatban az ultra-könnyű gépek tervezésénél is alkalmazzák.

Szárnyon ébredő légerők, siklószám.

“Az áramlásra szögben állított és megfelelően kialakított testeken az áramlás irányára merőleges erő is keletkezik” – írja a “Vitorlázórepülő oktatási segédlet”. Szárnyszelvények esetében ez az erő sokkal nagyobb, mint az áramlással párhuzamos. Van egy része az áramlásnak, amely elérve a szárnyat szinte beleolvad a szárny felületébe és eltűnik. Ez a semleges szál, mely a T₁ torló pontban éri el a szárnyat és a T₂ hátsó torló pontban újra megjelenik. A fölötte levő légtömeg a szárnyat felülről, az alatta levő pedig alulról kerüli meg, és a kilépő él után kissé lefelé térítődik el.

Minden levegőben mozgó testre légellenállás hat. Ez az erő egyenes arányban áll a homlokfelülettel, a közeg sűrűségével, és az áramlási sebesség négyzetével (ρ=1,23 kg/m³):

Olyan testek esetén, amelyeken az áramlás irányára merőlegesen is ébred erő, az A vonatkozási felületnek az alaprajzi területét veszik. Ezen erőt a test geometriai kialakítása és felületének kiképzése egyaránt befolyásolja. A szárnyon keletkező légerők eredője F_r nem merőleges az áramlásra, ezért két erőre szokás bontani: F_y felhajtó erőre és F_x ellenállásra. Az erők felbontásának szabályai alapján:

Ez lehetővé teszi, hogy a szárnyak tulajdonságainak vizsgálata során csak a szárnyak szelvényeit vegyük figyelembe, és csak az eredő légerő- (c_r), felhajtóerő- (c_y) és ellenállás- (c_x) tényezőket vizsgáljuk. Ezen tényezőket szélcsatornás mérések segítségével szokták meghatározni. A tényezők értékei erősen változhatnak az áramlás szögének függvényében. Különösen igaz ez a megállapítás az ívelt testekre (mint pl. profilozott szárny).

A szárny légellenállása két fő alkotóból áll. Az egyik az alaki vagy nyomásellenállás, melynek lényege, hogy a mozgó tárgy előtt túlnyomás – torló nyomás képződik, – és az áramvonalak az akadály előtt kitérnek. A kiugró peremeken, meredeken táguló légterületeken, vagy súrlódás hatására lassuló áramlatokban a hirtelen lokális nyomásnövekedésnek köszönhetően az áramlások visszafordulnak a felületnél, leválnak, örvények keletkeznek, melyek energiát vonnak el a rendszerből. A mozgó tárgy mögött negatív nyomású területek képződnek. Ez a két nyomás együttesen fékezi a tárgy haladását a levegőben.
Levegőben mozgó tárgyakra, ugyanúgy mint szilárd testek esetében, súrlódási erők hatnak. A súrlódási ellenállás a szilárd testekkel ellentétben nem a test és a közeg, hanem a közeg eltérő sebességgel mozgó rétegek között jön létre (egy jól képzett szárny összes ellenállásának akár 85%-át is kiteheti). A tesztek azt is kimutatták, hogy a hosszabb húrhosszal rendelkező szárny súrlódási ellenállás-tényezője kisebb a rövidebbhez képest.

Az ellenállás nagyságát az áramlás típusa is befolyásolja: a turbulens határréteg súrlódási ellenállása ugyan nagyobb, de a leválások később következnek be, emiatt a test ellenállása kisebb lehet, mint a lamináris határréteg esetében.

Egy repülőgép szárnyának minőségére, légerőtani jóságára a felhajtóerő és az ellenállás egymáshoz viszonyított nagyságából következtethetünk. Az sem mindegy, hogyan alakul a viszonyuk különböző állásszögeknél. Ebből kifolyólag a fejlesztések egyik célja, hogy a lehetőségekhez képest a felhajtóerő minél nagyobb legyen, miközben az előre haladást gátló ellenállást minimálisra szorítsák vissza. A minőség fokmérője tehát a siklószám, mely a két erő viszonyát adja meg: . Egy másik minőségi mutató a siklószög, mely a légerő eredőjének visszahajlási szögét mutatja qz áramlás normáljához (merőlegeséhez) képest: .

Nyomás eloszlása a szárnyszelvény körül. A szárny felületének domborúsága miatt az áramlás sebessége a húr hossza mentén nem állandó sem alatta, sem felette, ezért a nyomás értéke is eltérő. A felhajtóerőt előidéző nyomáskülönbséget kísérleti úton mérik (sok 1mm átmérőjű lyuk a szárnyfelületen, melyek nyomásmérő műszerre vannak kötve). A mérési eredményeket azután grafikonba öntik, melynek vízszintes tengelye a szelvény húrhosszának százalékos értékét, a függőleges pedig a viszonylagos nyomásértéket ábrázolja úgy, hogy fent a negatív nyomás különbséget, vagyis szívó erőt, lent pedig a megnövekedett nyomást mutatja. Az így kapott nyomáseloszlási képet több állásszögre is elkészítik.

A mérési eredmények alapján belátható, hogy a felhajtó erő nyomás különbség alkotta részének kétharmadát a szárny felett képződött alacsony nyomás, egyharmadát pedig a szárny alatt uralkodó magas nyomás adja (a szárny lényegében nem támaszkodik, hanem felszívja magát a fölötte levő rétegekre).

Aszimmetrikus áramlásnál növekvő állásszögek esetén a nyomáseloszlás is változik: a görbék csúcsa és a görbe alatti terület előre tolódik. Ennek az az oka, hogy a torló pont az orrpontja alá csúszik, ezért a semleges szál fölötti áramvonalaknak erősen fel kell gyorsulniuk, hogy kikerüljék az orr részt. Ez a változás a nyomás eredőjének a támadási pontját, a nyomásközéppont vándorlását okozza a profil húr mentén: A szárny feletti és alatti nyomáseloszlás eredőjét külön-külön képezve erőpárt kapunk, melyek eltérő pontokon fejtik ki hatásukat. Így a szárnyon forgatónyomaték képződik, mely nagy állásszögeknél a szárny belépő élét felfelé, kis és negatív szögeknél pedig lefelé csavarja (nem teljesen lineáris a függvény, ezért katalógusban kell ellenőrizni minden Re számra). Még akkor is, ha olyan α₀ szögben áll a szárny, melyben nem termel felhajtó erőt, vagyis a keletkező erők nagysága azonos, de ellentétes irányúak. Együttes hatásuk olyan nyomatékot hoz létre, mely a szárny orrát lefelé tolja, a kilépő élét pedig felfelé.

Főbb folyamatok áttekintésével ugyan még nem lettünk sokkal okosabbak a profilválasztás terén, de közelebb kerültünk a szárny működésének megértéshez. Innentől kezdve már csak a felhajtóerőről beszélünk, különböző paraméterek függvényében.

Follow