A modelltervezés talán legkritikusabb, legfontosabb művelete a megfelelő szárnyprofil kiválasztása. Lényegében több ezer profil áll rendelkezésünkre, de legjobb csak egy van. Igen ám, de mi van azokkal a szárnyakkal, melyeknél több profilt is alkalmaznak? Igazából legjobb nem is nagyon létezik, mivel minden gép más és más. Ezért itt csak az irányelvekről, illetve az egyes kategóriákban jól bevált szelvényekről beszélhetünk, mert minden profilválasztás szükségszerűen magával hozza a kompromisszumot. A megfelelő profil kiválasztása első sorban azon múlik, mennyire értjük meg a leíró adatokat, és mennyire ismerjük a trendeket. Az aktuális felhajtó erő, a szárny ellenállása és a nyomásközéppont vektora az alábbi hat plusz egy paramétertől függ, melyek közvetett/közvetlen módon kapcsolatban állnak a szelvény profiljának kialakításával:

Sebesség – mindhárom érték egyenes arányban változik a sebesség változás négyzetével.
Szárnyfelület – mindhárom adat egyenesen arányban áll a felület nagyságával.
Húr hossz – Reynolds szám és nyomásközéppont egyenesen arányos a szelvény hosszával.
Állás szöge – a hasznos tartományban (0-felhajtó erőtől átesésig), mindhárom érték nő, de nem lineárisan (az alaki ellenállás bizonyos tartományban csökkenhet) az állásszög növelésével.
Oldalviszony – egyenes arányban van mindhárom paraméter értékével.
Szárny formája – többdimenziós hatása van mindhárom tulajdonságra.

Reynolds szám (Re) – egy dimenzió nélküli szám, mely a kísérletben kialakított, és a gyakorlatban alkalmazott szelvény geometriai és áramlástani hasonlóságát adja meg. A szélcsatornában mért profil adatai akkor igazak a szárnyprofilunkra, ha a vizsgált alanyok geometriailag hasonlóak (a felület kiképzésében is) és a Reynolds számuk is azonos. Ezt a számot a test hossza (húr hossz) és áramlási sebesség (repülési sebesség) ismeretében könnyedén kiszámolható. Mivel ez a szám sok paramétertől függ, így csak közelítő, nagyságrendi számítást érdemes elvégezni. Ezt a gyakorlatban az ultra-könnyű gépek tervezésénél is alkalmazzák.

Szárnyon ébredő légerők, siklószám.

“Az áramlásra szögben állított és megfelelően kialakított testeken az áramlás irányára merőleges erő is keletkezik” – írja a “Vitorlázórepülő oktatási segédlet”. Szárnyszelvények esetében ez az erő sokkal nagyobb, mint az áramlással párhuzamos. Van egy része az áramlásnak, amely elérve a szárnyat szinte beleolvad a szárny felületébe és eltűnik. Ez a semleges szál, mely a T₁ torló pontban éri el a szárnyat és a T₂ hátsó torló pontban újra megjelenik. A fölötte levő légtömeg a szárnyat felülről, az alatta levő pedig alulról kerüli meg, és a kilépő él után kissé lefelé térítődik el.

Minden levegőben mozgó testre légellenállás hat. Ez az erő egyenes arányban áll a homlokfelülettel, a közeg sűrűségével, és az áramlási sebesség négyzetével (ρ=1,23 kg/m³):

Olyan testek esetén, amelyeken az áramlás irányára merőlegesen is ébred erő, az A vonatkozási felületnek az alaprajzi területét veszik. Ezen erőt a test geometriai kialakítása és felületének kiképzése egyaránt befolyásolja. A szárnyon keletkező légerők eredője F_r nem merőleges az áramlásra, ezért két erőre szokás bontani: F_y felhajtó erőre és F_x ellenállásra. Az erők felbontásának szabályai alapján:

Ez lehetővé teszi, hogy a szárnyak tulajdonságainak vizsgálata során csak a szárnyak szelvényeit vegyük figyelembe, és csak az eredő légerő- (c_r), felhajtóerő- (c_y) és ellenállás- (c_x) tényezőket vizsgáljuk. Ezen tényezőket szélcsatornás mérések segítségével szokták meghatározni. A tényezők értékei erősen változhatnak az áramlás szögének függvényében. Különösen igaz ez a megállapítás az ívelt testekre (mint pl. profilozott szárny).

A szárny légellenállása két fő alkotóból áll. Az egyik az alaki vagy nyomásellenállás, melynek lényege, hogy a mozgó tárgy előtt túlnyomás – torló nyomás képződik, – és az áramvonalak az akadály előtt kitérnek. A kiugró peremeken, meredeken táguló légterületeken, vagy súrlódás hatására lassuló áramlatokban a hirtelen lokális nyomásnövekedésnek köszönhetően az áramlások visszafordulnak a felületnél, leválnak, örvények keletkeznek, melyek energiát vonnak el a rendszerből. A mozgó tárgy mögött negatív nyomású területek képződnek. Ez a két nyomás együttesen fékezi a tárgy haladását a levegőben.
Levegőben mozgó tárgyakra, ugyanúgy mint szilárd testek esetében, súrlódási erők hatnak. A súrlódási ellenállás a szilárd testekkel ellentétben nem a test és a közeg, hanem a közeg eltérő sebességgel mozgó rétegek között jön létre (egy jól képzett szárny összes ellenállásának akár 85%-át is kiteheti). A tesztek azt is kimutatták, hogy a hosszabb húrhosszal rendelkező szárny súrlódási ellenállás-tényezője kisebb a rövidebbhez képest.

Az ellenállás nagyságát az áramlás típusa is befolyásolja: a turbulens határréteg súrlódási ellenállása ugyan nagyobb, de a leválások később következnek be, emiatt a test ellenállása kisebb lehet, mint a lamináris határréteg esetében.

Egy repülőgép szárnyának minőségére, légerőtani jóságára a felhajtóerő és az ellenállás egymáshoz viszonyított nagyságából következtethetünk. Az sem mindegy, hogyan alakul a viszonyuk különböző állásszögeknél. Ebből kifolyólag a fejlesztések egyik célja, hogy a lehetőségekhez képest a felhajtóerő minél nagyobb legyen, miközben az előre haladást gátló ellenállást minimálisra szorítsák vissza. A minőség fokmérője tehát a siklószám, mely a két erő viszonyát adja meg: . Egy másik minőségi mutató a siklószög, mely a légerő eredőjének visszahajlási szögét mutatja qz áramlás normáljához (merőlegeséhez) képest: .

Nyomás eloszlása a szárnyszelvény körül. A szárny felületének domborúsága miatt az áramlás sebessége a húr hossza mentén nem állandó sem alatta, sem felette, ezért a nyomás értéke is eltérő. A felhajtóerőt előidéző nyomáskülönbséget kísérleti úton mérik (sok 1mm átmérőjű lyuk a szárnyfelületen, melyek nyomásmérő műszerre vannak kötve). A mérési eredményeket azután grafikonba öntik, melynek vízszintes tengelye a szelvény húrhosszának százalékos értékét, a függőleges pedig a viszonylagos nyomásértéket ábrázolja úgy, hogy fent a negatív nyomás különbséget, vagyis szívó erőt, lent pedig a megnövekedett nyomást mutatja. Az így kapott nyomáseloszlási képet több állásszögre is elkészítik.

A mérési eredmények alapján belátható, hogy a felhajtó erő nyomás különbség alkotta részének kétharmadát a szárny felett képződött alacsony nyomás, egyharmadát pedig a szárny alatt uralkodó magas nyomás adja (a szárny lényegében nem támaszkodik, hanem felszívja magát a fölötte levő rétegekre).

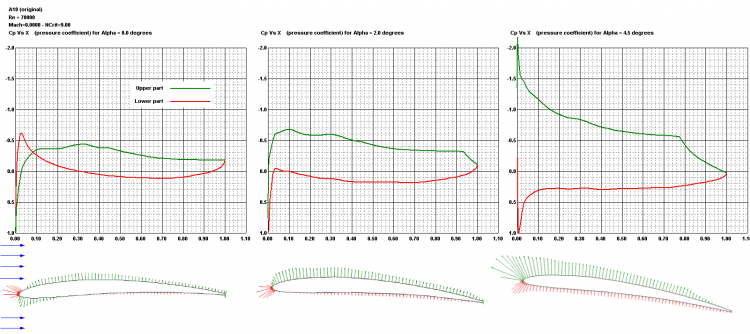
Aszimmetrikus áramlásnál növekvő állásszögek esetén a nyomáseloszlás is változik: a görbék csúcsa és a görbe alatti terület előre tolódik. Ennek az az oka, hogy a torló pont az orrpontja alá csúszik, ezért a semleges szál fölötti áramvonalaknak erősen fel kell gyorsulniuk, hogy kikerüljék az orr részt. Ez a változás a nyomás eredőjének a támadási pontját, a nyomásközéppont vándorlását okozza a profil húr mentén: A szárny feletti és alatti nyomáseloszlás eredőjét külön-külön képezve erőpárt kapunk, melyek eltérő pontokon fejtik ki hatásukat. Így a szárnyon forgatónyomaték képződik, mely nagy állásszögeknél a szárny belépő élét felfelé, kis és negatív szögeknél pedig lefelé csavarja (nem teljesen lineáris a függvény, ezért katalógusban kell ellenőrizni minden Re számra). Még akkor is, ha olyan α₀ szögben áll a szárny, melyben nem termel felhajtó erőt, vagyis a keletkező erők nagysága azonos, de ellentétes irányúak. Együttes hatásuk olyan nyomatékot hoz létre, mely a szárny orrát lefelé tolja, a kilépő élét pedig felfelé.

Főbb folyamatok áttekintésével ugyan még nem lettünk sokkal okosabbak a profilválasztás terén, de közelebb kerültünk a szárny működésének megértéshez. Innentől kezdve már csak a felhajtóerőről beszélünk, különböző paraméterek függvényében.

One Response to “Végtelen szárny aerodinamikája”

1. RC hangár » Profilok, diagramok, tulajdonságok says:

   2012. October 31 at 15:29

   […] a rendeltetése, hogy a repülőgép levegőben tartásához szükséges felhajtó erőt termeljen (Végtelen szárny aerodinamikája). E létrejötte és nagysága a szárny geometriai kialakulásától függ. A szárnyszelvény […]

   Log in to Reply